激光器可以在任何能够在适当能级之间实现“粒子数反转”的设备中实现。典型的设备是光学腔，但半导体也不应被排除在外。

　　负温度——亚稳态热力学状态

　　我们已经在之前的文章中讨论了所谓的“粒子数反转”导致的“负绝对温度”。

　　让我们简要回顾一下要点。对于一个具有N≫1个粒子的系统，其能量在两个能级ε=0(基态)，ε=E>0(第一激发态)上量子化，统计力学告诉我们，在热力学平衡(在温度T下)时，最密集的能级是基态ε=0。然而，从适当的分布函数的解析表达式可以推断出，替换T→−T会导致粒子数反转。这种情况并非形式上的，因为这种条件可以通过浸入磁场中的自旋系统来实现。

　　然而，这些是非平衡或亚稳态，因为系统倾向于恢复初始配置，其中基态是最密集的。在恢复过程中，系统发出的能量不超过反转粒子数级所需的能量。因此，亚稳态的存在并不违反能量守恒原理。

　　光学腔

　　我们如何创建一个具有N≫1个粒子的物理系统，在其中可以实现粒子数反转?除了上述自旋系统的例子外，还有共振腔的物理上有趣的情况，即一个配备有完美反射壁的腔，关于电磁场的传播。众所周知，这样的系统具有对应于驻波(共振频率)的离散频率谱。

　　在所讨论的情况下，我们感兴趣的是光学腔或具有可见区域特征频率的共振腔。现在让我们想象一下，在这个腔中填充大量相同的原子(典型的数量级是10^20)。从热力学的角度来看，我们有一个与腔壁在给定温度T下处于热平衡的系统，我们假设后者使得单个原子处于基态，我们用E1表示。

　　在时刻t=0，我们在腔内激活一个可见区域的电磁场。一个以频率ν振荡的驻波场。从量子角度来看，我们可以使用含时微扰理论[1]单独处理原子，因为每个原子都受到一个随时间变化的外部场，这反过来决定了电子跃迁E1→En，使得En−E1=hν。

　　在这种情况下，光学腔模拟了前一节中提出的两能级系统。因此，实现粒子数反转的可能性被打开。在光学腔的情况下，我们将反转通过光学泵浦获得，其中泵浦由电磁场组成。

　　对应于粒子数反转的热力学状态是亚稳态，因此系统倾向于恢复初始粒子数，并伴随发射相同频率ν的电磁辐射。发射辐射的单色性随之而来。更具体地说，单个原子独立地发射能量量子hν。在波传播方面，用ψj(x,t)表示第j个原子发射的辐射场的通用分量，我们在复数表示法中有：

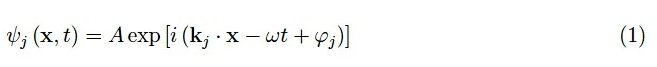
　　其中：A是振幅;kj是波矢;ω=2πν是角频率;ϕj是相位。单色平面波具有共同的振幅和频率，但没有传播方向和相位。确切地说，如果I是入射在单个原子上的辐射强度，存在一个临界(或阈值)值IS，对于I

　　统计上，ϕj被描述为一个具有平坦功率谱(白噪声)的随机变量。由于N≫1，离散分布ϕj很好地近似于一个连续分布ϕ(j)，如前所述，这是一个白噪声，如图1所示。ϕ(j)的自相关函数是一个狄拉克δ函数，因此除了原点外处处为零。物理上这意味着ϕ从原子j到原子j′的值之间没有相关性。

　　对于强度I∼IS，自相关函数偏离了预测的δ形趋势，ϕ(j)呈现出典型的布朗噪声趋势(图2)。对于I>IS，量ϕ(j)变成一个确定性变量：发射的单个波列的相位之间存在相关性。超过阈值值的进一步特征是单个波列沿由波矢k定义的相同方向传播。

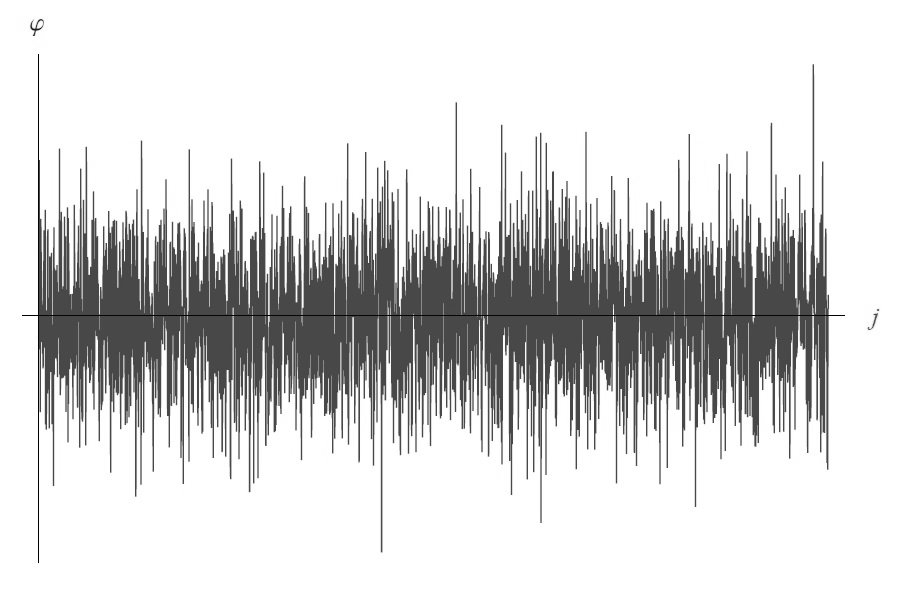
　　由N个原子发射产生的场是一个相干场Ψ(x,t)，前提是ϕj是确定性的，即对于I>IS。相反，低于阈值值，单个波列的叠加描述了一个非相干辐射场。

　　对于I>IS，我们创建了一个激光器(Light Amplification by Stimulated Emission of Radiation的缩写)。在激光阈值以下，N个发射之间的相位相关性(即相干性)的破坏是热源的典型特征，这些热源由黑体模型表示：灯泡和恒星的发射光谱缺乏相干性。更准确地说，黑体也可以从一个具有完美反射壁并在温度T下处于平衡的腔中创建。为了测量这个系统发射的单色辐射，需要配备一个适当的滤波器。然而，如上所述，辐射在上述意义上是非相干的，并且模拟了灯泡的钨丝或恒星等离子体的发射。

　　从热力学的角度来看，激光器处于亚稳态，因此我们被迫不关闭决定粒子数反转的电磁场，这因此成为一个不可逆过程(否则，发射的能量可以自发地重新用于更多地填充能级E1，从而触发新的激光循环)。如前一节所述，这并不违反能量守恒原理，系统是耗散的，但属于非典型类别，因为它从环境中(泵浦)吸收无序能量，然后发射有序能量。这里的“有序/无序”二分法指的是发射辐射的相干性和入射辐射的非相干性。

　　我们是否可能面临一个违反热力学第二定律(更广为人知的熵增定律)的系统?激光循环的不可逆性(除非向系统释放能量)意味着熵的增加。然而，有序能量的发射将意味着熵的减少，因为这一量是物理系统无序程度的度量。在当前的知识状态下，这个问题是开放的，主要是因为我们处理的是远离平衡的热力学系统，由于由此产生的微分方程的非线性，这些系统在数学上几乎难以处理。顺便说一下，这种行为似乎是生物等复杂系统的典型特征。对这些主题感兴趣的读者可以参考伊利亚·普里高津的出版物，他是首批研究远离平衡的热力学系统的学者之一2。

　　半导体

　　迟早会发生，这是不可避免的。它发生了……没有人会知道为什么。也许一个电子没有穿过晶格到另一个，由于来自太阳的X射线光子或高能宇宙射线，尽管有保护。(G. Harry Stine，又名Lee Correy的《星际驾驶员》)

　　第1节中描述的系统适合进行有趣的推广。确切地说，我们不再考虑具有离散能谱的N≫1个粒子的系统，而是尝试创建具有连续能谱的N≫1个粒子的系统。一个典型的例子是由半导体给出的，这些半导体具有连续的单粒子能谱，尽管被带隙分隔开。

　　另一方面，在之前的教程中，我们确立了从热力学的角度来看，半导体的行为主要由导带中的电子决定。后者构成了一个“理想的费米气体”，或者是完美气体的一个特例，因为电子之间的库仑排斥与正离子施加的吸引力相比可以忽略不计，正离子的周期性势能反过来决定了单电子能谱的带结构。

　　然后我们引入了“空穴”的概念，定义为“电子的缺失”。这一概念唯一地确定了空穴能级的统计分布，从电子的分布开始，我们在这里重写：

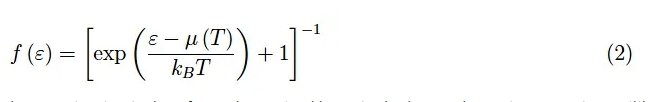
　　因此，所研究的半导体被简化为一个在温度T和化学势µ(T)下处于平衡的单一热力学系统。然而，在更现实的描述中，我们有一个第二热力学系统，即在温度T下占据价带能级的电子，如图3所示。

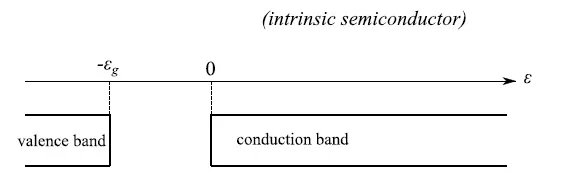
　　请注意，这些电子以共价键成对结合，但作为第一近似，我们可以认为这种键的强度可以忽略不计(实际上，在室温下，热能足以打破大量的共价键)，因此通过理想费米气体进行简化。由此出现了由图4图形表示的一对(Sc, Sv)热力学系统，连接它们的连续线概述了各个系统的传热和扩散接触。换句话说，它们交换能量和粒子。关于后者，可以想到共价键的断裂，导致电子转移到价带，或者随机事件，如能量>εg的光子，撞击晶体后从共价键中释放电子。

　　可以合理地假设一种热平衡但非扩散平衡的条件，为此各自的化学势具有不同的值，尽管由相同的温度T决定。各自的分布函数如下：

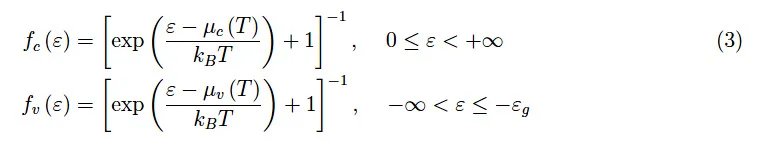
　　扩散过程主要涉及载流子的迁移和复合，因此假设热平衡是合理的，因为过量载流子复合过程的特征时间从10^-3秒到10^-9秒不等。相比之下，Sv和Sc(或晶体的任何子系统对)之间的热平衡在10^-12秒的时间间隔内达到。因此，在半导体中，热化过程在复合过程的时间尺度上是即时的。

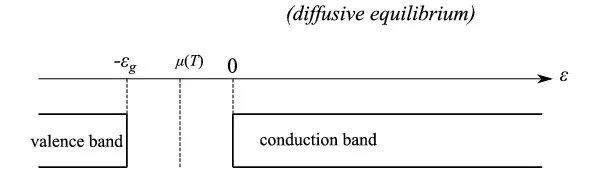
　　在图5中，两个系统Sv和Sc达到了扩散平衡，其特征是化学势µ(T)的唯一值，对于不太高的T，该值位于带隙中间。在图6中，上述系统处于热平衡但非扩散平衡。

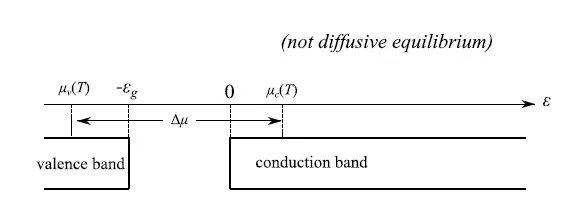
　　此时，很明显，可以通过某种手段(例如，通过电子注入)实现粒子数反转。激活激光循环的必要条件由不等式fc(0)>fv(−εg)给出，这保证了粒子数反转。从方程(3)立即得出µc(T)−µv(T)>εg，即，各自的化学势之差必须大于带隙(图7)。

浮思特科技专注功率器件领域，为客户提供IGBT、IPM模块等功率器件以及MCU和触控芯片，是一家拥有核心技术的电子元器件供应商和解决方案商。