基于回旋共振的实验技术用于测量半导体中载流子的有效质量，但在金属中效果不佳。在本教程中，我们将研究一些俄罗斯物理学家测试的类似技术。

　　费米表面

　　在前一期中，我们看到在Sommerfeld模型中，金属的导电电子的能量ε接近费米能量εF。由于这是一个半经典模型，因此引用费米速度vF和相对轨迹(规避海森堡不确定性原理)是合理的。换句话说，在上述模型中，量子效应融入了费米-狄拉克统计分布，而不是单个电子的动力学。因此，该模型被称为半经典模型。

　　我们将e表示为动量(或冲量)p = mev 的函数：

　　从中，可以唯一定义费米冲量：

　　下一步是应用德布罗意假设(旧量子理论)：与电子相关的物质波是一个平面波，其传播向量为：

　　方程(1)变为：

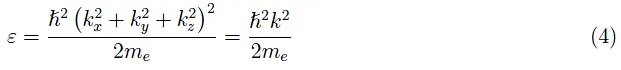
　　这又将单个电子的能量表示为德布罗意波的传播向量的笛卡尔分量的函数。因此，我们得到一个包含三个实变量的实函数，其图形位于R4中(无法可视化)。然而，我们可以描绘上述函数的等能量面，这些面称为等能面。更精确地说，如果ε0是允许的能量值，则相应的等能面为：

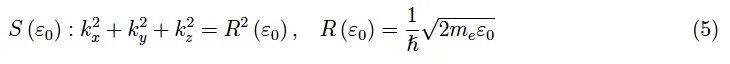
　　也就是说，这是一个以k空间原点为中心的球体(三维欧几里得空间)，半径为R(ε0)。特别地，费米球是表面S(εF)。具有量子知识的读者会将波数k = |k|视为“良好的量子数”，因为k唯一定义了单个电子的量子态，专门参考统计分布，而忽略自旋。ε的唯一定义源于对k的函数依赖性，如方程(4)所表达。

　　由于在k空间中，能量ε的分布是各向同性的，因而e通过其模与k相关，因此相应的等能面(球体)上的点代表物理上不同的状态，但具有相同的能量。在量子力学中，这通过声称能级ε是简并的，并且具有无限的简并度来表达。更精确地说，即等于上述表面的点数。然而，我们必须考虑自旋的自由度。一般来说，由自旋引起的简并度写为gs = 2s + 1，其中s是所考虑粒子的自旋。在电子的情况下，s = 1/2，因此gs = 2;实际上，任何自旋为1/2的状态k(即被自旋向上的电子占据)与波数k相同但自旋为1/2(自旋向下)的状态是不同的。

　　这两种状态具有相同的能量;因此，额外的简并度等于2。注意，泡利不相容原理并没有被违反，因为上述状态在物理上是不同的。而且，由于它们是无限多的，每个状态占据着一对自旋向上和向下的电子，因此可以考虑与所考虑的晶体的理论无限延展相兼容的几乎无限数量的电子(以不破坏晶格的周期性)。

　　根据Sommerfeld模型，贡献于金属电导率的电子是那些在k空间的费米球上“分配”的状态。此状态的分布是各向同性的，因此对于替换k -> -k是对称的。由于k通过方程(3)与单个电子的动量p相关，整体动量为零，因此电流流动(电流密度)也为零。施加均匀的静电场E，转化为作用在单个电子上的恒定力F = eE。

　　根据动量定理，电子动量随时间的变化δt为δp = Fδt，这对应于方程(3)中的δk。因此，电场的作用是将费米球在k空间中平移。这破坏了各向同性，因此也破坏了k和-k之间的对称性。结果是非零的总动量，因此电荷的净流动。电场瞬时关闭将重建初始配置(没有电流)，将费米球的中心移动到k空间坐标系的原点。这是通过涉及电子-晶格碰撞的统计机制几乎瞬时发生的。

　　金属中的回旋共振

　　在之前的教程中，我们看到在半导体中，测量由于施加均匀的磁静场B0而引起的回旋频率ωc是通过测量沿B0传播的平坦单色电磁波的吸收来实现的。在金属的情况下，由于以下原因，这种技术难以实施：

　　除非使用频率ω > ωp(其中ωp是与导电电子密度n成正比的等离子频率)，否则金属几乎完全反射电磁波。由于金属的n大约是1023 cm−3，因此ωp的数量级约为1016 rad/s，对应的频率fp约为104 GHz。

　　频率ω > ωp的电磁波的穿透深度δ相对较低(皮肤效应)。频率f = 1 GHz时，δ的典型值约为10−5 cm;δ在给定金属中定义了所谓的皮肤区域。

　　如前所述，在大多数金属中，费米表面并不是球形的。这破坏了单个电子能量分布相对于k的各向同性。因此，通过改变B0的方向，可以得到不同的回旋频率。

　　一些俄罗斯物理学家测试的技术包括使用一个金属板，施加与板平面平行的磁场B0。通过这种方式，单个电子的轨迹轴包含在上述平面内。

　　注：此技术的变体是由Azbel-Kaner几何提供的。

　　射频场垂直于B0发送。如果R0 > δ(其中R0是单个回旋轨道的半径)，那么只有一部分轨道将受到电磁场的作用。然而，穿越皮肤区域的电子可以从电磁场吸收能量，从而加速。在相反的情况下(即如果它向电场释放能量)，它会减速。在回旋加速器(粒子加速器)中会发生类似的机制;因此，电磁学文献中称ωc为“回旋频率”，也称为拉莫尔频率。

　　因此，我们期望吸收峰(共振)，但是在电子向射频场释放能量的情况下也是如此。具体来说，电子在与B0垂直的平面上的周期性运动的投影必须与电磁场同相位。如果Tc = 2π/ωc是上述运动的周期，T = 2π/ω是电磁场的周期，则必须满足Tc = nT，其中n是正整数。回忆回旋频率ωc的表达式，我们得到共振条件：

　　此条件返回磁静场B0的值，其中电子与射频场处于共振状态。在碱金属的情况下，费米表面大约是球形的，针对不同的n > 1值测量B0的值，从而通过方程(6)获得有效质量，然后对获得的结果进行平均。对于在氦温度下的铜，见参考文献。

　　结论

　　回旋共振实验不仅可以测定金属和半导体中载流子的有效质量，还为研究费米表面的拓扑提供了极好的工具。

浮思特科技专注功率器件领域，为客户提供IGBT、IPM模块等功率器件以及MCU和触控芯片，是一家拥有核心技术的电子元器件供应商和解决方案商。